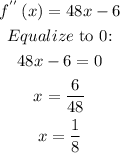Question

Let f(x) = 8x^3-3x^2Then f(x) has a relative minimum atx= __a relative maximum atx=___and infection point atx=___

Answer 1

`\begin{gathered} f\mleft(x\mright)\text{ has a relative minimum at x=1/4} \\ f\mleft(x\mright)\text{ has a relative maximum at x=0} \\ f\mleft(x\mright)\text{ has an inflection point at x=1/8} \end{gathered}`

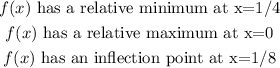
Explanation:

To find the relative minimum and maximum, find the first derivate of the following function:

`f\mleft(x\mright)=8x^3-3x^2`

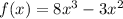
Derivating, using the derivative of a sum is equal to the sum of the derivatives. f'(x)=g'(x)+h'(x)

`f^(\prime)\left(x\right)=24x^2-6x`

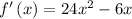
A relative maximum point is a point where the function changes direction from increasing to decreasing. Similarly, a relative minimum point is a point where the function changes direction from decreasing to increasing.

Equalize the first derivable to 0.

`\begin{gathered} 24x^2-6x=0 \\ 6x\left(4x-1\right)=0 \\ 6x_1=0 \\ x_1=0 \\ \\ 4x_2-1=0 \\ x_2=(1)/(4) \end{gathered}`

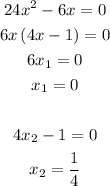
Then, the x-coordinate of the relative minimum is x=1/4, and the x-coordinate of the relative maximum is x=0.

The inflection point is a point of a curve at which a change in the direction of curvature occurs. To find the inflection points, find the second derivate and solve for equals 0:

`\begin{gathered} f^{^(\prime)^(\prime)}\left(x\right)=48x-6 \\ Equalize\text{ to 0:} \\ 48x-6=0 \\ x=(6)/(48) \\ x=(1)/(8) \end{gathered}`