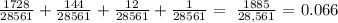Answer:
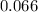
Step-by-step explanation:
Here, we want to get the probability that at least 1 ace is drawn
There are 4 aces in a deck of cards
The total number of cards is 52
This means we have a total of 48 non-ace cards
The probability of picking at least an ace means that:
1 ace, 3 others
or 2 aces, 2 others
or
3 ace, 1 other
or
4 ace, no other
These are all the possible pickling combinations
The probability of picking an ace is the number of ace cards divided by the total number of cards which are 4/52 = 1/13
For non-ace cards, we have the probability as 48/52 = 12/13
We are going to add the combinations
We have that as follows:
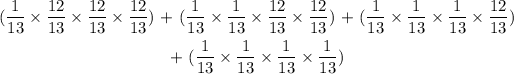
Finally, we simply the above so as to get a single fraction
We have that as follows: