Question

What is the maximum number of possible extreme values for the function,f(x) = x - 7x-6?O A. 1O B. 2O c. 4O D. 3

Answer 1

Do youSOLUTION

Step 1 :

We are meant to find the extreme values of the function f,

`\text{set f}^1\text{ ( x ) = 0 and solve.}`

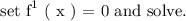
This will give us the x - coordinates of the extreme values / local maximum and minimum.

Step 2 :

Considering the function,

`f(x)=x^2\text{ - 7 x - 6 .}`

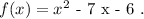
We need to find the minimum value of f ( we know it is minimum because the parabola opens upwards) , we set :

`\begin{gathered} f^1\text{ ( x ) = 2x - 7 = 0 } \\ \text{Solving, we get 2 x = 7} \\ \text{x = }(7)/(2)\text{ = 3. 5 is the location of the minimum.} \end{gathered}`

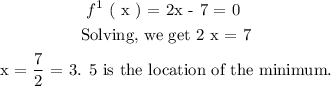
Step 3 :

To get the y - cordinate , we need to find f ( 3. 5 ) :

`\begin{gathered} f(3.5)=(3.5)^2\text{ - 7 ( 3 . 5 ) - 6 } \\ =\text{ 12.25 - 24. 5 - 6} \\ =\text{ -18. 25} \end{gathered}`

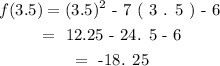
Therefore, the extreme minimum of f occurs at the point ( 3. 5 , - 18. 25 )