Question

an ice cube is freesinf in such a way thag ghe side length s,in inches, is s(t)=1/2t+2 where t is in hours. The surface area of the ice cube is the function A(s)=6s^2. Part A: Write an equstion that gives the volume at t hours after freezing begins. Part B: Find the surface area as the function kf time, using composition, and determjne its range.Part C: After how many hours will the surface area equak 216 squRs inches? Show all neccesady calculations.

Answer 1

Part A

we have the function

`S(t)=(1)/(2)t+2`

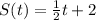
Remember that

The volume of a cube is given by the formula

`V=S^3`

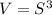
substitute the function S(t) in the formula of volume

`V(t)=((1)/(2)t+2)^3`

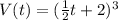
Part B

Find the surface area as the function of time

we have

`SA(S)=6S^2`

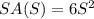
Find out (SAoS)(t)=SA(S(t))

so

`SA(S(t))=6((1)/(2)t+2)^2`

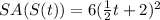
Part C

we have

SA=216 in2

using the function of Part B

`\begin{gathered} SA(t)=6((1)/(2)t+2)^2 \\ \\ 6((1)/(2)t+2)^2=216 \end{gathered}`

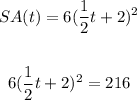
Solve for t

`\begin{gathered} ((1)/(2)t+2)^2=(216)/(6) \\ \\ ((1)/(2)t+2)^2=36 \\ take\text{ square root on both sides} \\ \\ (1)/(2)t+2=\pm6 \\ \\ (1)/(2)t=-2\pm6 \\ \\ t=-4\pm12 \end{gathered}`

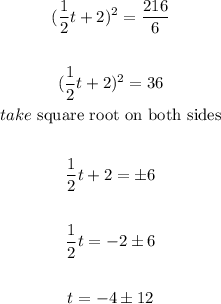
The values of t are

t=8 hours and t=-16 hours ( is not a solution because is a negative number)

therefore

The answer is 8 hours