Part A
we have the function

Remember that
The volume of a cube is given by the formula
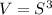
substitute the function S(t) in the formula of volume

Part B
Find the surface area as the function of time
we have
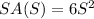
Find out (SAoS)(t)=SA(S(t))
so
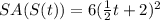
Part C
we have
SA=216 in2
using the function of Part B

Solve for t
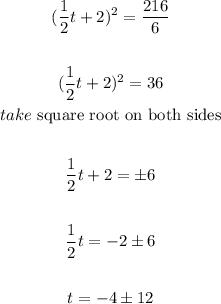
The values of t are
t=8 hours and t=-16 hours ( is not a solution because is a negative number)
therefore
The answer is 8 hours