Part A:
For a normally distributed data, population mean = sample mean
From the question, population mean = 34.82
Hence the sample mean = 34.82
The sample standard deviation is given by;
![\sigma_x=\text{ }\frac{\sigma}{\sqrt[]{n}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/yk3dz9buqznoaq2klstmfj4ld0bwfrs5b5.png)
where n = 6, and
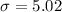
![\sigma_x=\frac{5.02}{\sqrt[]{6}}\text{ = 2.05}](https://img.qammunity.org/2023/formulas/mathematics/high-school/rvk1iv3mb2jhvnzxa1cps8ra6qgvztizu3.png)
Therefore, the sample standard deviation is 2.05.
Part B
The interpretation of the standard deviation of the sampling distribution is that, since the square root of the sample size appears at the denominator, the standard deviation decreases as the sample size increases.
Part C

Hence, the probability is 0.0111.