Question

Consider the function f(x) = 3x + 8x ^ - 1 For this function there are four important intervals: (- infty,A],[A,B),(B,C] and [C, infty) where A, and Care the critical numbers and the function is not defined at

Answer 1

Given the following function:

`f(x)=3x+8x^(-1)`

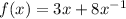
We will find the critical points A and C and the point B at which the function is not defined

First, we will find B:

f(x) is a rational function

The domain will be the real numbers except for the zeros of the denominator

The denominator has a zero at x = 0

So, when x = B = 0, the function will not be defined

B = 0

Second, we will find A and C

We need to find the first derivative df/dx and then solve the equation df/dx=0

`(df)/(dx)=3-8x^(-2)`

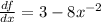
Now, solve the equation df/dx = 0

`\begin{gathered} 3-8x^(-2)=0 \\ 3-(8)/(x^2)=0 \\ \\ (8)/(x^2)=3 \\ \\ x^2=(8)/(3)\to x=\pm\sqrt{(8)/(3)}=\pm(2√(6))/(3) \end{gathered}`

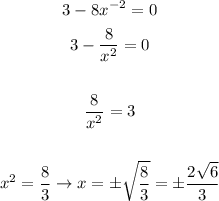
So, the values of A and C will be as follows:

`\begin{gathered} A=-(2√(6))/(3) \\ \\ C=(2√(6))/(3) \end{gathered}`

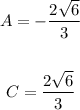
So, the answer will be:

`\begin{gathered} A=-(2√(6))/(3) \\ \\ B=0 \\ \\ C=(2√(6))/(3) \end{gathered}`

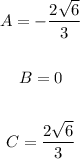
( -∞, A) : Increasing

(A, B) : decreasing

(A, C) : decreasing

(C, ∞) : Increasing

(-∞, B): Concave down

(B, ∞): concave up