The mirror image of a line about origin will be obtained by replacing x with -x and y with -y.
Therefore, the mirror image of the line 4y = 3x + 7 will be:
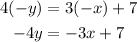
Rearranging the equation, we have:
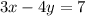
Note that a dilation always preserves parallelism. Therefore, any image formed from the preimage must have the same slope.
Therefore, we can say that the dilation will yield the equation:
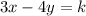
where k is a constant.
Going by this, the equation that can represent its image will be:
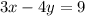
OPTION 1 is correct.