From the graph
We have the points
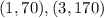
First, we are to find the slope
To slope will be calculated using

From the given points we have
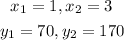
Therefore, the slope is

Therefore, the slope is 50
Next we are to apply point slope form formula
The formula is given as

By putting the values we have
We get the equation of the function as follows
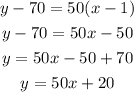
Therefore, the linear function is y = 50x + 20
Finind the vertical intercept
The vertical intercept is the value of y at x = 0
Putting x = 0 in the linear function we have
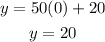
The vertical intercept = 20