Question

A grocer wants to mix two kinds of candy. One kind sells for $2.00 per pound, and the other sells for $2.85 per pound. He wants to mix a total of 21 pounds and sell it for $2.05 per pound. How many pounds of each kind should he use in the new mix?

Answer 1

Let x be the number of pounds of the $2.00 candy and let y be the number of pounds of the $2.85 candy.

We know that in total the grocer wants 21 pounds, this can be express by the equation:

`x+y=21`

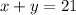
We also know that the grocer wants the mix to cost $2.05 per pound. This condition can be express as:

`\begin{gathered} 2x+2.85y=2.05\cdot21 \\ 2x+\text{2}.85y=43.05 \end{gathered}`

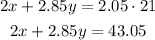
Hence we have the system of equations:

`\begin{gathered} x+y=21 \\ 2x+2.85y=43.05 \end{gathered}`

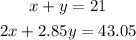
To solve ithe system we solve the first equation for y:

`y=21-x`

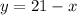
and we plug this value in the second equation:

`\begin{gathered} 2x+2.85(21-x)=43.05 \\ 2x+59.85-2.85x=43.05 \\ -0.85=43.05-59.85 \\ -0.85x=-16.8 \\ x=(-16.8)/(-0.85) \\ x=19.76 \end{gathered}`

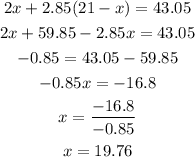
Now we plug the value of x in the expression for y we found earlier:

`\begin{gathered} y=21-19.76 \\ y=\text{1}.24 \end{gathered}`

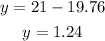
Therefore, the grocer needs 19.76 pounds of the $2.00 candy and 1.24 pounds of the $2.05 candy