The inequality given is:
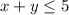
In order to graph this inequality, we need two points that will show us where the line (x+y = 5) is.
The easiest points to get are the values of x and y when the other is zero i.e.
The value of x when y = 0 to give (x, 0) as one point and
The value of y when x = 0 to give (0, y) as the second point.
This is done below:
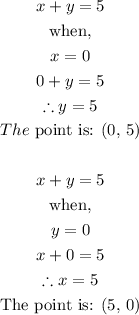
So now we have two points: (0, 5) and (5, 0)
Also in order to plot these points for the inequality, we need to know which part of the graph should be discarded.
We will also use these two points but this time, with the inequality sign.
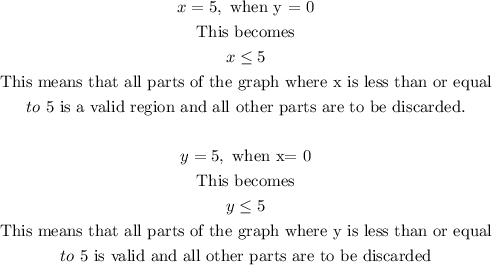
Because the inequality is less than or equal to, we must make the line solid instead of dashed
Now let us sketch this inequality:
Comparing this with the options,
The final answer is: Option D