Question

The table gives a set of outcomes and their probabilities. Let A be the event "the outcome is less than 6". Let B be the event "the outcome is divisible by 3". Are A and B independent events? Outcome Probability 1 0.1 2 0.2 3 0.2 4 0.2 5 0.2 6 0.1 yes no

Answer 1

In order to have independent events, we need to verify the following formula:

`P(A\cap B)=P(A)\cdot P(B)`

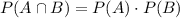
For event A, the outcomes that are less than 6 are 1, 2, 3, 4 and 5, so the probability of event A is:

`\begin{gathered} P(A)=P(1)+P(2)+P(3)+P(4)+P(5) \\ P(A)=0.1+0.2+0.2+0.2+0.2 \\ P(A)=0.9 \end{gathered}`

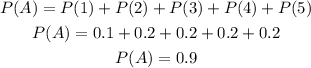
For event B, the outcomes that are divisible by 3 are 3 and 6, so:

`\begin{gathered} P(B)=P(3)+P(6) \\ P(B)=0.2+0.1 \\ P(B)=0.3 \end{gathered}`

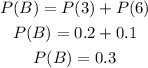
The intersection of these events is only number 3, so:

`P(A\cap B)=P(3)=0.2`

Verifying the formula, we have:

`\begin{gathered} 0.2=0.9\cdot0.3 \\ 0.2=0.27 \end{gathered}`

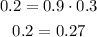
The result is false, so the events are not independent, therefore the answer is NO.