Question

The conjugate of (y + 3) is (y + 3)?

Answer 1

Hello there. To solve this question, we have to remember some properties about conjugates and real (complex) numbers.

Suppose the expression

`y+3`

Is a real number, hence we know that

`y`

must also be a real number because the real numbers are a field and they are closed under addition.

The conjugate of a real number is then the real number itself, which means that

`\overline{y+3}=y+3`

Otherwise, if y is a complex number, it means it's imaginary part is not equal to zero.

Assuming y = a + bi for a, b real numbers and b not equal to zero, we have that

`y+3=a+bi+3=(a+3)+bi`

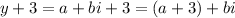
Hence the conjugate of this number is

`\overline{(a+3)+bi}=(a+3)-bi`

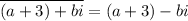
That is equivalent to have

`\overline{y}+3`

If y is a complex number.