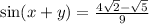Question

Find sin(x + y)given: sin x = − 2/3 and x is in Quadrant III; and sin y = 1/3 and y is in Quadrant II.

Answer 1

Given

sin x = − 2/3 and x is in Quadrant III; and sin y = 1/3 and y is in Quadrant II.​

Find

sin(x + y)

Step-by-step explanation

sin x = − 2/3 and x is in Quadrant III

as, cos x is negative in Quadrant III

`\begin{gathered} \cos x=-√(1-\sin^2x) \\ \\ \cos x=-\sqrt{1-(-(2)/(3))^2} \\ \\ \cos x=-\sqrt{1-(4)/(9)} \\ \\ \cos x=-\sqrt{(5)/(9)} \\ \\ \cos x=(-√(5))/(3) \end{gathered}`

sin y = 1/3 and y is in Quadrant II.​

cos y is negative in Quadrant II.​

`\begin{gathered} \cos y=-√(1-\sin^2xy) \\ \\ \cos y=-\sqrt{1-((1)/(3))^2} \\ \\ \cos y=-\sqrt{1-(1)/(9)} \\ \\ \cos y=-\sqrt{(8)/(9)} \\ \\ \cos y=(-2√(2))/(3) \end{gathered}`

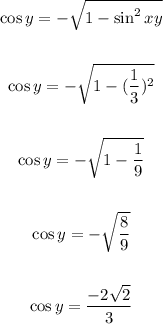
as we know the formula of

sin (x + y)= sinx cosy + cosx siny

now put values ,

`\begin{gathered} \sin(x+y)=\sin x\cos y+\cos x\sin y \\ \\ \sin(x+y)=(-(2)/(3))((-2√(2))/(3))+((-√(5))/(3))((1)/(3)) \\ \\ \sin(x+y)=(4√(2))/(9)-(√(5))/(9) \\ \\ \sin(x+y)=(4√(2)-√(5))/(9) \end{gathered}`

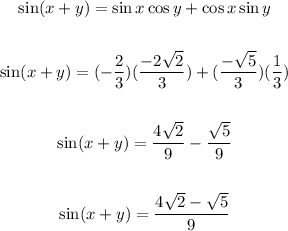
Final Answer

`\sin(x+y)=(4√(2)-√(5))/(9)`