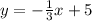To find the equation of the line in its slope-intercept form, you can take two points through which the line passes, find the slope of the line, and then use the point-slope formula.
For example, you can take the points (0,5) and (6,3).
The formula to find the slope of the line is
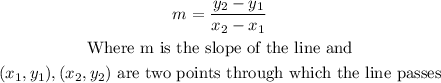
So, you have

Now using the point-slope formula you have
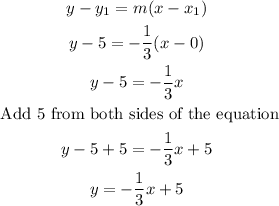
The equation of a line in its slope-intercept form is
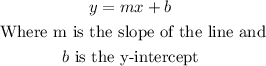
Therefore, the equation of the line shown in the graph, in its slope-intercept form is