Given:
The explicit formula is,
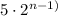
To find:
First three terms
Step-by-step explanation:
Substituting n = 1 in the explicit formula, we get
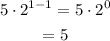
Substituting n = 2 in the explicit formula, we get

Substituting n = 3 in the explicit formula, we get
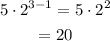
Hence the first three terms of the geometric sequence are 5, 10, and 20.
Final answer:
The first three terms of the geometric sequence are 5, 10, and 20.