The number of students in a homeroom is

The number of posts to be chosen from is
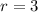
Concept:
The above selection can be done using the permutation formula below
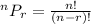
By substituting the values, we will have
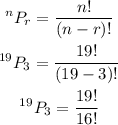
By expanding the factorial, we will have
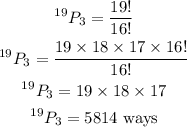
Hence,
The final answer is = 5,814 ways