Question

Graph the Following features on the graphSlope = 2Y-intercept = -2

Answer 1

Since we have been given a slope and a y-intercept, we can conclude the graph is a line.

The slope-intercept form of an line equation is as follows:

`y=mx+b`

Where m is the slope and b is the y-intercept.

Since we have been given these, we can write the equation for this line as:

`y=2x-2`

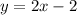
To draw a line, we need two points only. Since we have the equation, we can choose any value of x and input into it to get is corresponding y value. We can also do it the other way around.

Let's choose x = 0 and x = 1, for example.

For x = 0, we will have the y value:

`\begin{gathered} y=2x-2 \\ y=2\cdot0-2=0-2=-2 \end{gathered}`

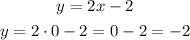
Thus, we have the point x = 0, y = -2, that is, (0, -2).

For x = 1, we have:

`\begin{gathered} y=2x-2 \\ y=2\cdot1-2=2-2=0 \end{gathered}`

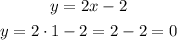
So, we have the point x = 1, y = 0, that is, (1, 0).

Now, we can plot these points and connect them to graph the line: