Given:
The function is f(x) =kx^4+8x^2.
The function has zero at x = 2.
Step-by-step explanation:
The function has zero at x = 2, so f(2) = 0.
Determine the value of k by using f(2) = 0.

So function is,
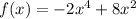
For the zeros of the function f(x) = 0. So,
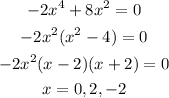
So other roots of the function is 0 and -2.
Answer:
Value of k is -2
Other roots: 0 and -2