Question

(a). A particle, whose acceleration is constant, is moving in the negative x direction at a speed of 4.36 m/s, and 10.9 s later the particle is moving in the positive x direction at a speed of 7.94 m/s. Find the acceleration?(b). what will be the velocity 10.9 second before it was moving in the negative x directionat the speed of 4.36 m/s(c). when is the particle at rest. express this answer as a time in seconds elapsed since it was moving in the negative x-direction at a speed of 4.36 m/s.

Answer 1

(a). Given data:

* The velocity of the particle in the negative x-direction is,

`v_i=-4.36ms^(-1)`

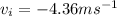
* The velocity of the particle in the positive x-direction is,

`v_f=7.94ms^(-1)`

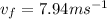
* The time taken by the particle is,

`t=10.9\text{ s}`

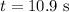
Solution:

The acceleration in terms of velocity and time is,

`a=(v_f-v_i)/(t)`

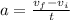
Substituting the known values,

`\begin{gathered} a=(7.94-(-4.36))/(10.9) \\ a=(7.94+4.36)/(10.9) \\ a=1.128ms^(-2) \end{gathered}`

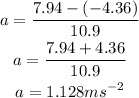
Thus, the acceleration of the particle is 1.128 meter per second squared.

(b). The velocity before the 10.9 second of the -4.36 m/s velocity is,

`\begin{gathered} a=(v_f-v)/(t) \\ 1.128=\frac{-4.36-v_{}}{10.9} \\ 12.295=-4.36-v \\ -v=12.295+4.36 \\ -v=16.655 \\ v=-16.655ms^(-1) \end{gathered}`

Thus, the value of the velocity is -16.655 meter per second.

(c). Let at time t particle will come to rest,

The time t in terms of acceleration is,

`\begin{gathered} a=(v_f-v_i)/(t) \\ 1.128=\frac{0-(-4.36)_{}}{t} \\ t=(4.36)/(1.128) \\ t=3.865\text{ s} \end{gathered}`

Thus, the particle will come to rest after 3.865 s since the velocity 4.36 m/s in negative x-axis.