Question

Find a_1 for the sequence with the given terms. a_3= 20 and a_5=80a_1

Answer 1

In general, the explicit formula of a geometric series is

`a_n=a_{}r^(n-1)`

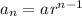
Where a and r are constants, and a_n is the n-th term.

In our case,

`\begin{gathered} a_3=20 \\ \text{and} \\ a_3=ar^(3-1)=ar^2 \\ \Rightarrow ar^2=20 \end{gathered}`

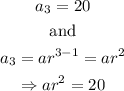
On the other hand,

`\begin{gathered} a_5=80 \\ \text{and} \\ a_5=ar^(5-1)=ar^4 \\ \Rightarrow ar^4=80 \end{gathered}`

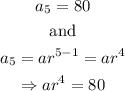
Use the two equations to find a and r, as shown below

`\begin{gathered} ar^2=20 \\ \Rightarrow r^2=(20)/(a) \\ \Rightarrow a(r^2)^2=80 \\ \Rightarrow a((20)/(a))^2=80 \\ \Rightarrow(400)/(a)=80 \\ \Rightarrow a=5 \end{gathered}`

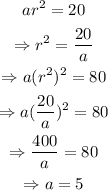
Finding r,

`\begin{gathered} a=5 \\ \Rightarrow5r^2=20 \\ \Rightarrow r^2=4 \\ \Rightarrow r=\sqrt[]{4}=\pm2 \end{gathered}`

Thus, the explicit formula is

`a_n=5(\pm2)^(n-1)`

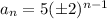
Set n=1 and find a_1 as shown below,

`\begin{gathered} n=1 \\ \Rightarrow a_1=5(\pm2)^(1-1)=5 \\ \Rightarrow a_1=5 \end{gathered}`

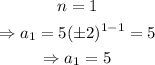
The answer is a_1=5