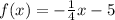Question

Find an equation of the line passing through the given points . Use function notation to write the equation(-8,-3) and (-12,-2) f(x)=

Answer 1

Given

Two points (-8,-3) and (-12,-2)

we are to find the equation of the line

Solution

Steps to find the equation of a line from two points:

1. Find the slope using the slope formula. ...

2. Use the slope and one of the points to solve for the y-intercept (b). ...

3. Once you know the value for m and the value for b, you can plug these into the slope-intercept form of a line (y = mx + b) to get the equation for the line.

Step 1

`\begin{gathered} \text{Formula for Slope(M)} \\ M=\frac{y_2-y_1}{x_2-x_1_{}} \end{gathered}`
`\begin{gathered} x_1=-8_{} \\ x_2=-12 \\ y_1=-3 \\ y_2=-2 \end{gathered}`
`\begin{gathered} M=(y_2-y_1)/(x_2-x_1) \\ M=(-2-(-3))/(-12-(-8)) \\ \\ \\ M=(-2+3)/(-12+8) \\ \\ \\ M=(1)/(-4) \end{gathered}`

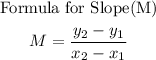
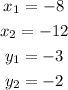
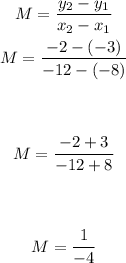
Step 2

Now, the y-intercept is b

`\begin{gathered} b=y_1-m.x_1 \\ b=\text{ -3 -(}(-1)/(4))(-8) \\ b=\text{ -3}-2 \\ b=-5 \end{gathered}`

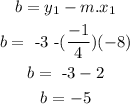
Step 3

`\begin{gathered} y=mx_{}+b \\ y=-(1)/(4)x-5 \end{gathered}`

The final answer

`f(x)=-(1)/(4)x-5`