Question

Which two line are parallel? how do you know A.2x-y=5 B.2x+y=3 C.y=2x+3

Answer 1

To know if two lines are parallel when defined in the xy-plane is to compare the slopes.

If the slopes are equal, the lines are parallel.

In order to compare the slopes, we need to put them in the form:

`y=mx+b`

Then, we have for A:

`\begin{gathered} 2x-y=5 \\ y=2x-5 \end{gathered}`

B.

`\begin{gathered} 2x+y=3 \\ y=-2x+3 \end{gathered}`

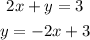
C.

`y=2x+3`

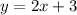
The only lies that have the same slope, hence, they are parallel, are A and C (slope: 2).

Note: B is perpendicular to A and C as the slope of B is the slope of A but opposite sign (multiplied by -1).