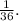To answer this question we will use the following expression to compute the probability that an event occurs:
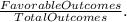
Then, the probability that Rebecca selects one poodle is:
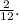
Simplifying the above result we get:
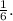
Since the pet store replaces the puppy with a puppy of the same breed, then the probability that Aaron selects one poodle is:
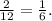
Therefore the probability that they both select a poodle is:
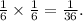
Answer: