Given:
The function is given
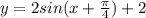
Required:
Find the amplitude and graph the function.
Step-by-step explanation:
compare the equation with the equation
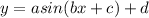
Where a = amplitude
period =
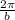
Phase shift =
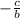
Vertical shife = d
Compare the given equation with the standard equation we get
a = 2, b = 1,
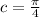
d = 2
Period
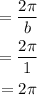
Phase shift
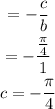
Vertical shift d = 2