Question

In exactly one year, how many mice would there be at school? EXPLAIN FULLY AND SHOW ALL WORK:Equation: Y=a(4)^xWhere:a is the initial value (when the generation = 0)x is the generation.

Answer 1

We know that each generation takes approximately 3 weeks, then, we can estimate how many generations we do have in one year, remember that one year has

`1\text{ year }\approx52.14286\text{ weeks}`

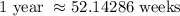
Then, in one year we have

`(52.14286)/(3)=17.383\text{ generations}`

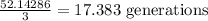
In the real world, we can't have half of a generation or a decimal generation, then, let's approximate it to the nearest integer, in that case, 17 generations.

We have the expression that predicts the number of mice, then we can use that equation to find the result for 17 generations:

`\begin{gathered} \text{ Initial Mice:} \\ f(x)=2\cdot4^x \end{gathered}`

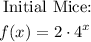
Evaluate that at x = 17

`\begin{gathered} \text{ Initial Mice} \\ f(x)=2\cdot4^x\Rightarrow f(17)=2\cdot4^(17)\Rightarrow3.44×10^(10) \end{gathered}`

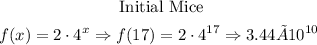
With an offspring of

`\begin{gathered} \text{ Offspring} \\ f(x)=6\cdot4^x\Rightarrow f(17)=6\cdot4^(17)=1.03×10^(11) \end{gathered}`

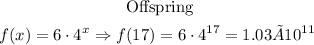
And the ending mice

`\begin{gathered} \text{ Ending Mice} \\ f(x)=8\cdot4^x\Rightarrow f(17)=8\cdot4^(17)=1.37×10^(11) \end{gathered}`

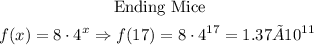
Therefore, the final answer is

`\text{ Ending mice = }1.37*10^(11)`