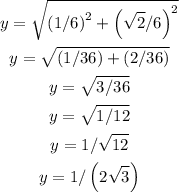Question

How do I find the values of x, y, and z?

Answer 1

Okay, here we have this:

Considering the provided figure, we are going to find the missing sides, so we obtain the following:

Then according to the altitude rule we obtain the following equality:

(1/3)/x = x/(1/6)

Let's solve for x:

x^2=(1/3)(1/6)

x^2=1/18

x=√(1/18)

x=1/√18

x=1/(3√2)

x=√2/6

Now let's find the other two missing sides using the Pythagorean theorem:

`\begin{gathered} z=\sqrt{\left((1)/(3)\right)^2+\left((√(2))/(6)\right)^2}^ \\ z=√(\lparen1/9)+\left(2/36\right)) \\ z=√(\left(1/9\right)+\left(1/18\right)) \\ z=√(\left(2/18\right)+\left(1/18\right)) \\ z=√(3/18) \\ z=√(1/6) \\ z=1/√(6) \end{gathered}`

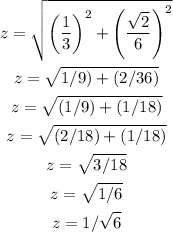
Finally let's find y:

`\begin{gathered} y=\sqrt{\left(1/6\right)^2+\left(√(2)/6\right)^2} \\ y=√(\left(1/36\right)+\left(2/36\right)) \\ y=√(3/36) \\ y=√(1/12) \\ y=1/√(12) \\ y=1/\left(2√(3)\right) \end{gathered}`