Question

I need help with my home work I rlly don't understand it

Answer 1

Let us call the price of the apple a.

The balance is lower on the left, which means

`0.25+0.60>0.45+a`

this says that the banana and the strawberries on the right side of the balance cost more than the orange and the apple on the left side.

Adding the numbers on the left gets us

`0.85>0.45+a`

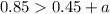
subtracting 0.45 from both sides gives

`0.45>a`

which can also be written as

`a<0.45`

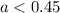
which means the price of apples is less than $0.45.

PART IV.

A situation similar to the one above is the following.

The circles (which can be balls) cost $1 and the price of triangular toys we do not know. This situation gives us the inequality

`3x+2Subtracting 2 from both sides gives is [tex]3xand subtracting x from both sides gives[tex]2x<1`

and finally dividing both sides by 2 gets us

`x<(1)/(2)`

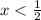
Hence, the price of triangular toys must be less than $0.5.