ANSWER:
-1 and -2/3
Explanation:
We have the following equation:
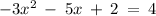
We rearrange the equation and it looks like this:
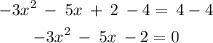
We apply the quadratic formula which is the following:
![\begin{gathered} x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{ in this case} \\ a=-3 \\ b=-5 \\ c=-2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/f1zit5xw8cmkk2bbem051jbv4ba4c9a004.png)
we replace and calculate the values of x:
![\begin{gathered} x_(1,2)=\frac{-(-5)\pm\sqrt[]{(-5)^2-4\cdot(-3)\cdot(-2)}}{2\cdot(-3)} \\ x_(1,2)=(5\pm1)/(-6) \\ x_1=(5+1)/(-6)=(6)/(-6)=-1 \\ x_2=(5-1)/(-6)=(4)/(-6)=-(2)/(3) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8h11we175ipgqlokcy1nj2nkjgzrmy45z3.png)
Therefore the solution of the equation is -1 and -2/3