Question

Ten granola bars and twelve bottles of water cost $23. Five granola bars and four bottles of water cost $10. How much do one granola bar and one bottle of water cost?$ Part BFor a fundraiser, a group plans to sell granola bars and bottles of water at the same prices as described in Part A. The group wants the income from the fundraiser to be at least $150.Choose the inequality to show the number of granola bars x and the number of bottles of water y that must be sold.A.1.4x + 0.75y > 150B.1.4x + 0.75y ≥ 150C.1.4x + 0.75y < 150D.1.4x + 0.75y ≤ 150

Answer 1

We want to find the cost of a granola bar and a water bottle. Let x be the cost of the granola bar and y the cost of the water bottle. We are told that 10 granola bars and 12 bottles of water cost 23. As x is the cost of one granola bar, 10 x is the cost of 10 granola bars. So if we add the cost of the granola bars and the cost of the water bottles we get the total cost. This leads to the equation

`10x+12y=23`

Now, if we calculate the equation for the other situation (5 granola bars and 4 bottles are 10) we get the equatio

`5x+4y=10`

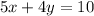
Let us multiply the second equation by 2. So we get

`10x+8y=20`

Now, we can subtract the second equation from the first one, so we ge t

`10x+12y\text{ - (10x+8y)=4y=23-20=3}`

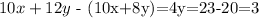
so if we divide both sides by 4, we get

`y=(3)/(4)=0.75`

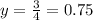
so the cost of one water bottle is 0.75

Now we replace this value in the first equation, so we get

`10x+12\cdot(3)/(4)=23=10x+9=23`

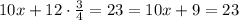
If we subtract 9 from both sides we get

`10x=23\text{ -9=14}`

So if we divide both sides by 10, we get

`x=(14)/(10)=1.4`

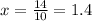
so the cost of a granola bar is 1.4

Now, we know that a granola bar costs 1.4 and a water bottle costs 0.75. If we sell x granola bars, the total income for x granola bars would be 1.4x. In the same manner, the total income for y water bottles would be 0.75y. If we add this two quantities we get

`1.4x+0.75y`

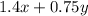
as this quantity should be at least 150, this means that it is greater than or equal to 150, so we get the inequality

`1.4x+0.75y\ge150`

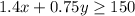
which is option B