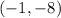Question

Solve the system of equations above using it elimination write your answer in the form (x,y) 8X + Y = -16-3X + Y = -5

Answer 1

Given the system of the equation below;

`\begin{gathered} 8x+y=-16----(1) \\ -3x+y=-5----(2) \end{gathered}`

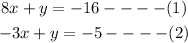
We can use the elimination method to solve the systems of equations

Step 1: Subtract equation 2 from equation 1 and solve for x

`\begin{gathered} 8x+y-(-3x+y)=-16-(-5) \\ 8x+y+3x-y=-16+5 \\ 11x=-11 \\ (11x)/(11)=-(11)/(11) \\ x=-1 \end{gathered}`

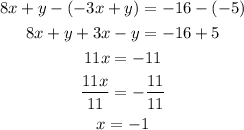
Step 2: Sustitute x = 1 in equation 1

`\begin{gathered} 8(-1)+y=-16 \\ -8+y=-16 \\ y=-16+8 \\ y=-8 \end{gathered}`

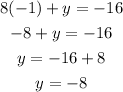
Therefore, the solution to the system of equation is

`(-1,-8)`