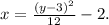The directrix and focus of a parabola are shown on the graph. Which is an equation for the parabola?X=-5

Question

asked Apr 8, 2023 71.7k views

1 Answer

Ramiromd · Answer 1 · 2023-04-12T16:02:10+0000

From the graph, we notice that the parabola has to be a horizontal parabola with vertex at:

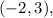
that opens to the right.

Recall that the standard form of a horizontal parabola is:

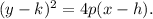
$\mleft(y-k\mright)^2=4p\mleft(x-h\mright)\text{.}$

Where, (h,k) are the coordinates of the vertex, and p is the distance to the vertex to focus.

Substituting the vertex in the above equation, we get:

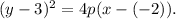
$(y-3)^2=4p(x-(-2))\text{.}$

From the diagram, we get that:

Therefore:

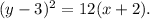
$(y-3)^2=12(x+2)\text{.}$

Solving the above equation for x, we get:

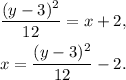
$\begin{gathered} ((y-3)^2)/(12)=x+2, \\ x=((y-3)^2)/(12)-2. \end{gathered}$

Answer: