We will first determine the sides of 2 & 3, that is:
![80=S^2_3\Rightarrow S_3=4\sqrt[]{5}](https://img.qammunity.org/2023/formulas/mathematics/college/5mol4m4n8wx5qgasiss7rl4zk6j9nc5lq1.png)
And:
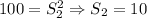
Where S2 and S3 are the sides of squares 1 and 2. From this we determine the side for square 1:
![S^2_2+S^2_3=S^2_1\Rightarrow(4\sqrt[]{5})^2+10^2=S^2_1\Rightarrow S_1=6\sqrt[]{5}](https://img.qammunity.org/2023/formulas/mathematics/college/sokv2lo9d0spitxctptfhvklxfmg9c0w7u.png)
Now, we determine the area of square 1, as follows:
![A_(s1)=(6\sqrt[]{5})^2\Rightarrow A_(s1)=180](https://img.qammunity.org/2023/formulas/mathematics/college/sixdichci4lxdlmzc1ji3b58ei77s9r59g.png)
So, we have that the area of square 1 equals 180 squared units.