Question

One canned juice drink is 15% apple juice; another is 5% apple juice. How manyliters of each should be mixed to get 10L that is 10% apple juice?

Answer 1

We have:

Let x = 15% apple juice

Let y = 5% apple juice

If you need 10% of 10L of apple juice or one liter of pure whole apple juice. This is:

`x+y=10`

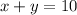
One canned juice drink is 15% apple juice; another is 5% apple juice. This can be expressed by:

`0.15x+0.05y=1`

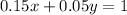
Then we solve the system of equations:

From equation 1

`\begin{gathered} x+y-y=10-y \\ x=10-y \end{gathered}`

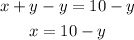
Substitute x in the second equation:

`\begin{gathered} 0.15(10-y)+0.05y=1 \\ Simplify \\ 1.5-0.15y+0.05y=1 \\ 1.5-0.1y=1 \\ solve\text{ for y} \\ 1.5-0.1y+-1.5=1-1.5 \\ -0.1y=-0.5 \\ (-0.1y)/(-0.1)=(-0.5)/(-0.1) \\ y=5 \end{gathered}`

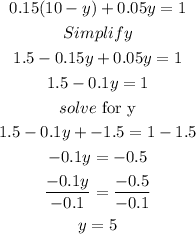
Next, substitute y in x:

`x=10-5=5`

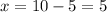
Answer: We need 5L of each apple juice.