Question

A wireless carrier offers the following plans that a person is considering. The Family Plan: $90 monthly fee, unlimited talk and text on up to 8 lines, and data charges of $40 for each device for up to 2 GB of data per device. The Mobile Share Plan: $120 monthly fee for up to 10 devices, unlimited talk and text for all the lines, and data charges of $35 for each device up to a shared total of 10 GB of data. Use P for the number of devices that need data plans as part of their cost.Find the model of the total cost of the Family Plan.Find the model of the total cost of the Mobile Share Plan.Assuming they stay under their data limit, find the number of devices that would make the two plans equal in cost.If a family has 3 smart phones, which plan is more affordable?To earn full credit please identify your variables and expressions you will be using to solve the problem. Show all work/calculations and thinking for each of the 4 parts.

Answer 1

For the family plan:

Let:

y1 = Total cost

a1 = Charge for each device = 40

b1 = Monthly fee = 90

P = Number of devices

So:

The model for the family plan will be given by:

`\begin{gathered} y1=a1P+b1 \\ y1=40P+90 \end{gathered}`

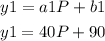
For the Mobile share plan:

Let:

y2 = Total cost

a2 = Charge for each device = 35

b2 = Monthly fee = 120

P = Number of devices

The model for the mobile share plan will be given by:

`\begin{gathered} y2=a2P+b2 \\ y2=35P+120 \end{gathered}`

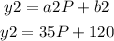
We can find the number of devices that would make the two plans equal in cost. Solving for:

`\begin{gathered} y1=y2 \\ 40P+90=35P+120 \\ solve_{\text{ }}for_{\text{ }}P\colon \\ 40P-35P=120-90 \\ 5P=30 \\ P=(30)/(5) \\ P=6 \end{gathered}`

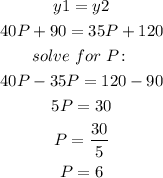
The number of devices that would make the two plans equal in cost is 6.

If P = 3

`\begin{gathered} y1=40(3)+90=210 \\ y2=35(3)+120=225 \end{gathered}`

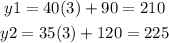
For 3 devices The family plan cost $210 and for 3 devices the mobile share plan cost $225, Therefore we can conclude that for 3 devices The family plan is more affordable.