Question

7. The vertex of a parabola is (5,-3) and another point on the parabola is (1,5). ** a. Write the equation for this parabola. b. Which of the following points is also on the parabola? (Show your work, of course) a) (0, 3) b) (-1, 9) c) (-1, 15) d) (7, 7)

Answer 1

The vertex form of the parabola is

`y=a(x-h)^2+k`

Where (h, k) are the coordinates of its vertex

Since the vertex of the parabola is (5, -3), then

h = 5 and k = -3

Substitute them in the form above

`\begin{gathered} y=a(x-5)^2+(-3) \\ y=a(x-5)^2-3 \end{gathered}`

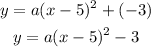
To find the value of (a) we will use the given point (1, 5)

Substitute x by 1 and y by 5

`\begin{gathered} 5=a(1-5)^2-3 \\ 5=a(-4)^2-3 \\ 5=16a-3 \end{gathered}`

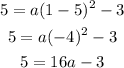
Add both sides by 3

`\begin{gathered} 5+3=16a-3+3 \\ 8=16a \end{gathered}`

Divide both sides by 16 to find (a)

`\begin{gathered} (8)/(16)=(16a)/(16) \\ (1)/(2)=a \\ a=(1)/(2) \end{gathered}`

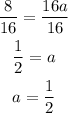
Substitute a by 1/2 in the equation above, then

a. The equation of the parabola is

`y=(1)/(2)(x-5)^2-3`

Let us substitute x and y in the equation by each answer

Since x = 0 and y = 3

`\begin{gathered} 3=(1)/(2)(0-5)^2-3 \\ 3=12.5-3 \\ 3=9.5 \\ \text{LHS}\\e RHS \end{gathered}`

Since x = -1 and y = 9

`\begin{gathered} 9=(1)/(2)(-1-5)^2-3 \\ 9=(1)/(2)(-6)^2-3 \\ 9=(1)/(3)(36)-3 \\ 9=12-3 \\ 9=9 \\ \text{LHS}=\text{RHS} \end{gathered}`

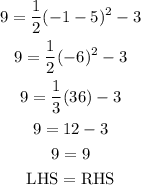
The point (-1, 9) lies on the parabola

The answer is b