Question

You plan to purchase a new car this week. The dealer offers you a loan at 1.6% interest compounded monthly for 6 years. Suppose you believe that you can afford to make payments of $350 per month based on your wages. a) How expensive of a car can you purchase in this situation if you borrow the entire purchase price? b) How much total interest would you have paid over the life of this loan if you do not choose to pay it off early?

Answer 1

The rule of the monthly payment is

`M\mathrm{}P=(P((r)/(n)))/(1-(1+(r)/(n))^(-nt))`

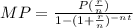
P is the initial amount of the loan

r is the rate in decimal

n is the period per time

t is the time

Let us find the value of them

r = 1.6% = 1.6/100 = 0.016

The interest is compounded monthly, then

n = 12

It is for 6 years, then

t = 6

The monthly payment is $350, Then

M.P = 350

let us substitute these values in the rule above to find P

`350=(P((0.016)/(12)))/(1-(1+(0.016)/(12))^(-12*6))`

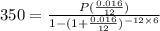
We will simplify it

`350=(P((1)/(750)))/(1-0.908522108)`
`350=(P((1)/(750)))/(0.09147789201)`

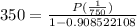
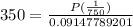
By using cross multiplication

`350*0.09147789201=P((1)/(750))`

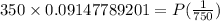
Multiply both sides by 750 to find P

`P=24012.94665`

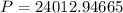
a) The Expensive of the care is $24012.94665

The total interest will be the difference between the total monthly payment and the purchase price

The total payment will be the monthly payment multiply by the number of months

`\begin{gathered} A=350*12*6 \\ A=25200 \end{gathered}`

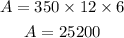
The Interset = 25200 - 24012.95 = 1187.05

b) The total interest is $1187.05