Question

Is this an arithmetic or geometricsequence?Starting at 10, each new term is 5/2 times the previous term.

Answer 1

Given:

First term = 10

Each new term is 5/2 times the previous term.

This implies that;

`\begin{gathered} first\text{ term, }a=10 \\ second\text{ term}=(5)/(2)*10=25 \\ third\text{ term}=(5)/(2)*25=62.5 \\ fourth\text{ term}=(5)/(2)*62.5=156.25 \end{gathered}`

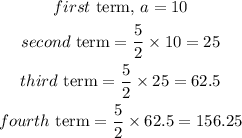
Calculate the common ratio between the successive terms,

`\begin{gathered} (25)/(10)=(62.5)/(25)=(156.25)/(62.5)=2.5 \\ \\ Hence,\text{ }r=2.5 \end{gathered}`

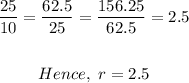
Since the successive terms are increasing by a common ratio, the sequence is a geometric sequence.