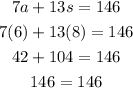Answer:
The cost of one adult ticket is $6 and the cost of one student ticket is $8.
Step-by-step explanation:
Let the cost of one adult ticket=a
Let the cost of one student ticket=s
They sell 7 adult tickets and 13 student tickets for a total of $146.
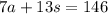
They sell $276 worth of tickets by selling 14 adult tickets and 24 student tickets.

Thus, the system of equations to model the scenario is:
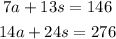
Multiply the first equation by 2 and the second by 1.
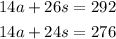
Subtract:

Next, we solve for 'a' using any of the equations.
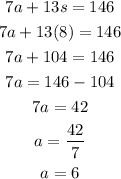
Therefore, the cost of one adult ticket is $6 and the cost of one student ticket is $8.
Check