1 Answer

Dylan Delobel · Answer 1 · 2023-05-24T14:27:31+0000

In order to solve this, we can use the trigonometric ratio of the cosine, which is given by the following expression:

$\cos \theta=(ac)/(h)$

Where ac is the adjacent leg to the angle θ and h is the length of the hypotenuse. By replacing 37° for θ, 17.3 for ac and x for h, we get:

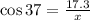
$\cos 37=(17.3)/(x)$

From this expression, we can solve for x to get:

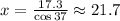
$x=(17.3)/(\cos 37)\approx21.7$

Then, x = 21.7

Please log in or register to add a comment.