Question

A vehicle purchased for $20,700 depreciates at a constant rate of 4%. Determine the approximate value of the vehicle 12 years after purchase. Round to the nearest whole dollar.

Answer 1

Given:

Initial value of vehicle = $20,700

Rate of depreciation = 4% = 0.04

Time, t = 12 years.

Let's find the value of the vehicle after the 12 years.

Let's apply the exponential decay formula:

`y=P(1-r)^t`

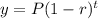
Where:

P = 20700

r is the rate of decay = 0.04

t is the time taken in years = 12 years.

Now, substitute these values into the equation and solve for y:

`\begin{gathered} y=20700(1-0.04)^(12) \\ \\ y=20700(0.96)^(12) \\ \\ y=20700(0.6127097573) \\ \\ y=12683.09\approx12683 \end{gathered}`

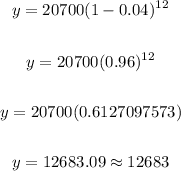
Therefore, the value of the vehicle 12 years after purchase is $12,683

• ANSWER:

$12,683