To find the Gibbs free energy of the reaction use the following formula:
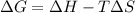
Where ΔG is the Gibbs free energy, ΔH is the enthalpy of reaction, ΔS is the reaction entropy and T is the absolute temperature.
Convert the given temperature to kelvin and then replace for the known values to find ΔG:
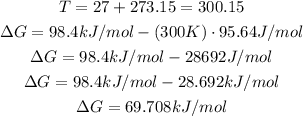
It means that the Gibbs free energy is 69.708kJ/mol.
According to this value (that is greater than 0) the reaction is not spontaneous at 27°C.