The correct graph is fourth option
Step-by-step explanation:
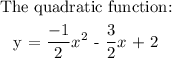
Using the intercepts: we have x-intercept and y-intercept
To get x intercept, we will equate the function to zero. That is y = 0
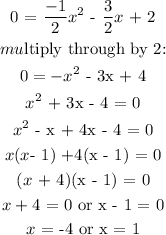
x intercepts are x = -4 and x = 1
This means the line will cross the x axis at two points: x = -4 and x = 1
To get y-intercept, we will equate x to zero:
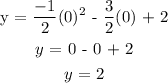
y-intercept = 2
This means the line will cross the y axis at y = 2
The correct graph is fourth option