Question

The function h is defined below.x² - 4x - 12h(x) =12x +322X-Find all values of x that are NOT in the domain of h.If there is more than one value, separate them with commas.

Answer 1

x=4,8

Step-by-step explanation:

Given the function, h(x) defined below:

`h(x)=(x^(2)-4 x-12)/(x^(2)-12 x+32)`

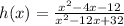
The values of x that are NOT in the domain of h are the values for which the denominator is 0, i.e.

`x^2-12x+32=0`

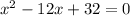
Solve the quadratic equation for x:

`\begin{gathered} x^2-8x-4x+32=0 \\ x(x-8)-4(x-8)=0 \\ (x-4)(x-8)=0 \\ x-4=0\text{ or }x-8=0 \\ x=4\text{ or }x=8 \end{gathered}`

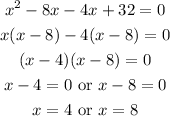
The values of x that are NOT in the domain of h are: x=4,8