we are given the following standard form of a function:
![f(x)=\sqrt[]{x-h}+k](https://img.qammunity.org/2023/formulas/mathematics/college/pm28npxctbhqc7wo2iqifj9i29nurdb4vf.png)
We are also given the following function:
![f(x)=\sqrt[]{x+2}+1](https://img.qammunity.org/2023/formulas/mathematics/college/xeu81kmpmkue2ejvvx5p0jhu4u24qrj8o6.png)
since "x - h" is the term under the radical, we have:
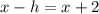
setting this value to zero, we get:

To solve for "x" we will subtract 2 to both sides:
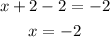
"k" is the value we add to the radical, therefore:
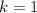
The starting point is:
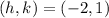
That is, up one, right two.