SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Find the value of KM
Using Pythagoras' Theorem,
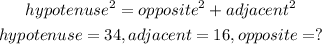
By substitution,
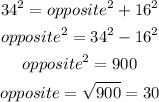
KM = 30
STEP 2: Find the required ratio
To get sin L:
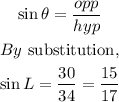
sin L = 15/17
To get cos L
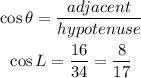
cos L = 8/17
To get tan L
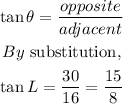
tan L = 15/8
STEP 3: Find the ratios for angle M
To get sin M
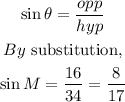
sin M = 8/17
To get cos M
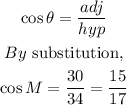
cos M = 15/17
tan L has been done in Step 2
tan L = 15/8