Question

an observer is 120 feet from the base of a television tower that is 140 ft tall. Find to the nearest degree the angle of elevation of the top of the tower from the point where the observer is standing

Answer 1

The angle of elevation is obtained as follows:

Step 1: Make a sketch of the scenario, as below?

Step 2: Apply the appropriate trigonometric ratio to obtain the unknown angle, as follows:

`\text{tan}\theta=(opposite)/(adjacent)`

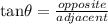
With respect to the unknown angle:

opposite = 140 ft

adjacent = 120 ft

Therefore:

`\begin{gathered} \text{tan}\theta=(opposite)/(adjacent) \\ \Rightarrow\text{tan}\theta=\frac{140\text{ ft}}{120\text{ ft}}=(140)/(120)=1.1667 \\ \Rightarrow\text{tan}\theta=1.1667 \\ \Rightarrow\theta=\tan ^(-1)(1.1667)=49.4^o \\ \Rightarrow\theta=49^o\text{ (to the nearest degre}e\text{)} \end{gathered}`

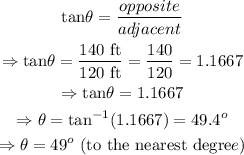
Therefore, the angle of elevation is 49 degrees