Question

5x+6y=-9 7x+2y=13 2x-9y=-10 3x+5y=22Show your work?

Answer 1

The first system of equations is

`\mleft\{\begin{aligned}5x+6y=-9 \\ 7x+2y=13\end{aligned}\mright.`

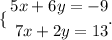
To solve this system, we multiply the second equation by -3, that way we'll be able to eliminate y and solve for x.

`\begin{gathered} \mleft\{\begin{aligned}5x+6y=-9 \\ -21x-6y=-39\end{aligned}\mright. \\ 5x-21x+6y-6y=-9-39 \\ -16x=-48 \\ x=(-48)/(-16)=3 \end{gathered}`

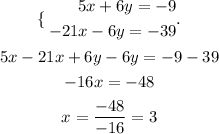
Then, we use the value of x to find y.

`\begin{gathered} 5x+6y=-9 \\ 5(3)+6y=-9 \\ 15+6y=-9 \\ 6y=-9-15 \\ 6y=-24 \\ y=(-24)/(6) \\ y=-4 \end{gathered}`

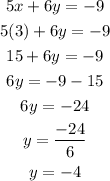
Therefore, the solutions are x = 3 and y = -4.

The second system of linear equations is

`\mleft\{\begin{aligned}2x-9y=-10 \\ 3x+5y=22\end{aligned}\mright.`

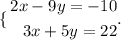
To solve this system, we multiply the first equation by -3/2.

`\begin{gathered} \mleft\{\begin{aligned}-3x+(27)/(2)y=15 \\ 3x+5y=22\end{aligned}\mright. \\ -3x+3x+(27)/(2)y+5y=15+22 \\ (27y+10y)/(2)=37 \\ (37y)/(2)=37 \\ y=(37\cdot2)/(37) \\ y=2 \end{gathered}`

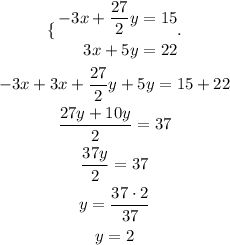
Then, we use this value to find x.

`\begin{gathered} 2x-9y=-10 \\ 2x-9(2)=-10 \\ 2x-18=-10 \\ 2x=18-10 \\ 2x=8 \\ x=(8)/(2) \\ x=4 \end{gathered}`

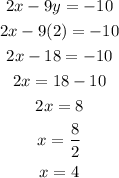
Therefore, the solutions are x = 4 and y = 2.