Question

Find the missing coordinates for the isosceles trapezoid.Ba, c)C(1,?)A(0,0)D(?,?)C = (b.D=(Word Bank:b-a a ba-b a + b c 0Blank 1:Blank 2:Blank 3:

Answer 1

From the figure

We have the folloing points

`A(0,0),B(a,c),C(b,-),D(-,-)_{}`

We need to find the missing points

Since the trapezoid is isosceles the side AB = Side CD

Considering coordinates B and C

let the missing point in C be z then

`\begin{gathered} B=(a,c) \\ C=(b,z) \end{gathered}`

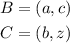
since Points B and C lie on the same y axis then

z = c.

Hence the coordinate C becomes

`C=(b,c)`

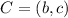
Next we need to find the missing points in D

let the missing x coordinate be x

let the missing y cordinate be y

Therefore

`D=(x,y)`

From the Graph,

The point Dlie on the x axis hence the coordinate of y is 0

hence y = 0

Therefore point D will become

`D=(x,0)`

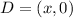
Finally we are to find the value of x

Recall that the trapezoid is isosceles

hence

`\text{length AB = length CD}`

Applying the formula for distance between two points

The formula is give as

`\text{Distance =}\sqrt[]{(x_2-x_1)^2-(y_2-y_1)^2}`

For points AB

A=(0,0), B = ( a,c)

Hence

`\begin{gathered} x_1=0,x_2=a \\ y_1=0,y_2=c \end{gathered}`

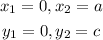
Therefore distance AB is

`\begin{gathered} AB=\sqrt[]{(a-0)^2+(c-0)^2} \\ AB=\sqrt[]{a^2+c^2} \end{gathered}`

For points CD

C = (b,c), D = (x,0)

Hence,

`\begin{gathered} x_1=b,x_2=x \\ y_1=c,y_2=0 \end{gathered}`

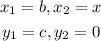
Therefore, distance CD is

`\begin{gathered} CD=\sqrt[]{(x-b)^2+(0-c)^2} \\ CD=\sqrt[]{(x-b)^2+c^2} \end{gathered}`

Recall distance AB = distance CD

Hence

`\begin{gathered} AB=CD \\ \sqrt[]{a^2+c^2}=\sqrt[]{(x-b)^2+c^2} \end{gathered}`

Simplifying further

we will get

`\begin{gathered} a^2+c^2=(x-b)^2+c^2 \\ a^2+c^2-c^2=(x-b)^2 \\ a^2=(x-b)^2 \\ \text{taking square root of both sides} \\ a=x-b \\ x=a+b \end{gathered}`

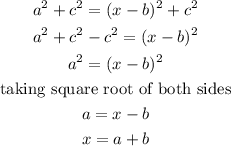
Therefore,

The coordinate of the point D is

`D=(a+b,0)`