Solution
This is a binomial probabilty problem
Let X be the event that your eggs are cracked. P(x) = 0.03
P(eggs that are not cracked)=1 - 0.03 = 0.97
For each egg, there is a probability that an egg cracked p = 0.03 that the egg is broken and a probability q = 1 - p = 0.97 that the egg is not cracked.
P(no more than two of your eggs are cracked)= P(zero eggs are cracked)+ P(1 egg is cracked) +P( 2 eggs are cracked)
P(at least one of your eggs are cracked) = P(X=0)
p = 0.03
q = 0.97
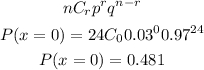
P(at least one of your eggs are cracked) = 1 - 0.481
P(at least one of your eggs are cracked) = 0.519